4.8 Trapezoidal rule

$$Area = \sum_{k=0}^{n-1} a_k = \sum_{k=0}^{n-1} \left[ \frac{1}{2} \left( f(x_{k+1}) + f(x_k) \right) \cdot (x_{k+1} - x_k) \right]$$

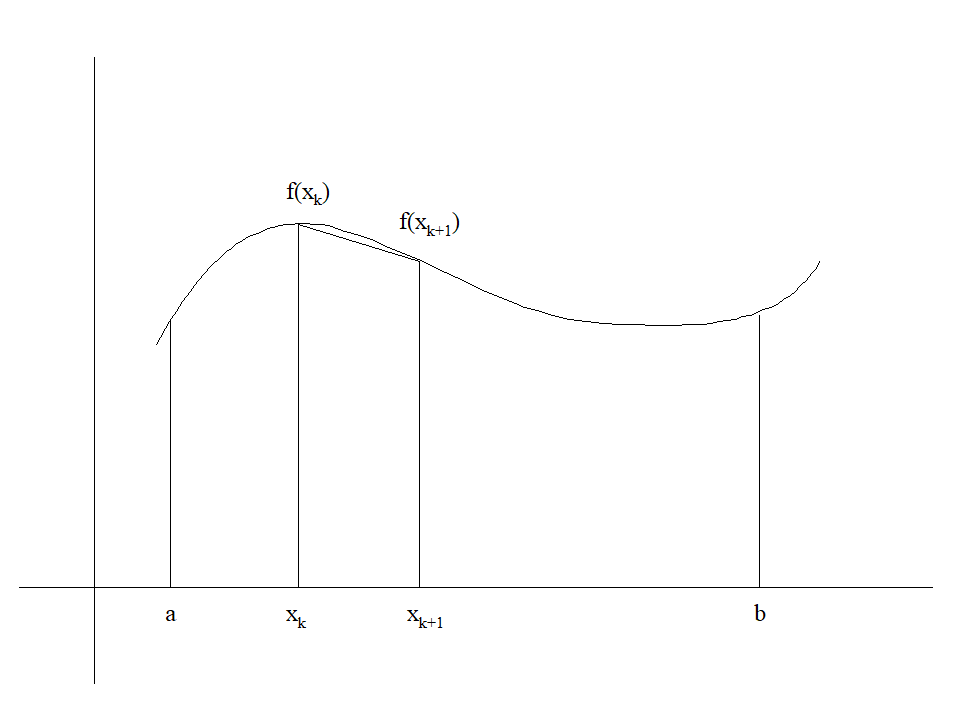
$$x_0 = a, \; x_n = b, \; x_k = a + \frac{b - a}{n} k$$

$$\int_a^b f(x) dx = \lim_{n \to \infty} \sum_{k=0}^{n-1} a_k \approx \sum_{k=0}^{n-1} a_k = \sum_{k=0}^{n-1} \left[ \frac{1}{2} \left( f(x_{k+1}) + f(x_k) \right) \cdot (x_{k+1} - x_k) \right]$$

• Exercise: Make an r function for trapezoidal approximation
• Exercise: Demonstrate the trapezoidal rule using MS-Excel

$$\begin{align*} h &= \frac{b - a}{n} \\ k &= 0, \cdots , n \\ a_k &= \frac{h}{2} (y_k + y_{k+1}) \end{align*}$$

$$\begin{equation} \begin{split} \int_a^b f(x) dx & \approx \sum_{k=0}^{n-1} a_k \\ & = h \left( \frac{y_0}{2} + y_1 + y_2 + \cdots + y_{n-1} + \frac{y_n}{2} \right) \end{split} \end{equation}$$

Practice script

trapez0 # with two sequences

## function (x, y) 
## {
##     n = length(x)
##     if (length(y) != n) 
##         return(NULL)
##     fi = vector()
##     for (i in 1:(n - 1)) {
##         fi[i] = (x[i + 1] - x[i]) * (y[i] + y[i + 1])/2
##     }
##     return(sum(fi))
## }
## <bytecode: 0x000001e2a3ab7ce8>
## <environment: namespace:math>

trapez1 # with function, a, b, n

## function (fx, a, b, n) 
## {
##     xk = seq(a, b, length.out = (n + 1))
##     fk = fx(xk)
##     Ar = (b - a)/n * (fk[1]/2 + sum(fk[2:n]) + fk[n + 1]/2)
##     return(Ar)
## }
## <bytecode: 0x000001e2a3b02010>
## <environment: namespace:math>

fx = function(x) exp(-x/100)
ifx = function(a, b) 100*exp(-a/100) - 100*exp(-b/100)

a = 0
b = 24
n = 10

ifx(a, b) # true value

## [1] 21.34

tPoints = c(0, 0.5, 1, 2, 3, 4, 6, 8, 12, 24)
y = fx(tPoints)
trapez0(tPoints,y)

## [1] 21.35

xk = seq(a, b, length.out=(n+1))
yk = fx(xk)
trapez0(xk, yk)

## [1] 21.34

trapez1(fx, a, b, n)

## [1] 21.34

trapez1(fx, a, b, 10*n)

## [1] 21.34