4.10 Romberg Integration

Using Richardson Extrapolation (a deffered approach to the limit)

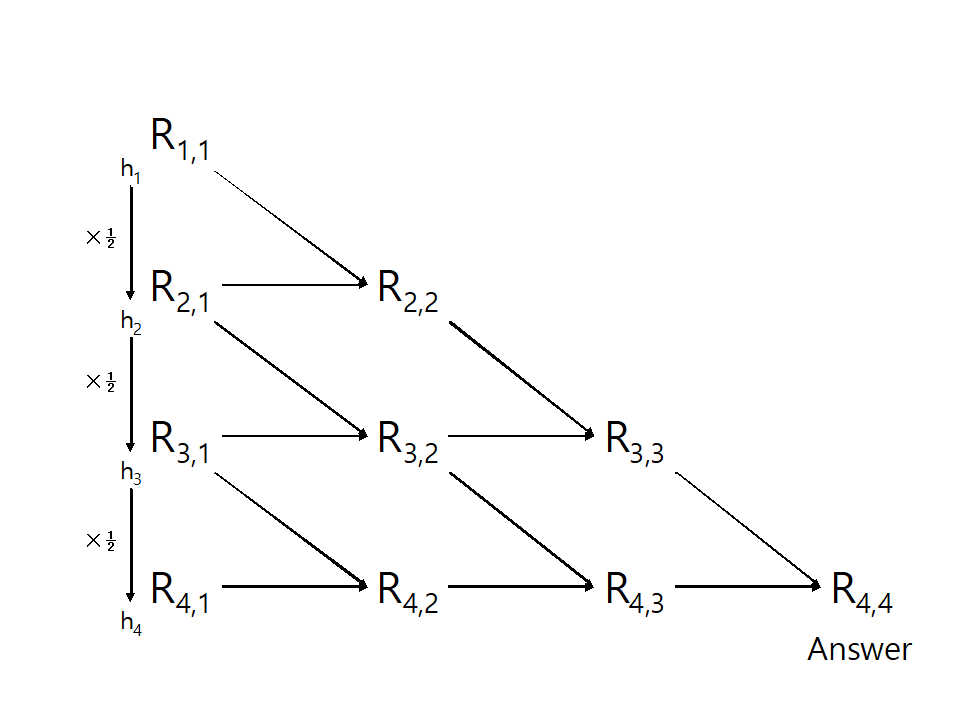
\[ h_1 = (b - a), \; h_2 = \frac{(b - a)}{2}, \; \cdots \; , h_n = \frac{(b - a)}{2^{n-1}} \]

\[\begin{align*} I_1 &= \frac{(b-a)}{2} \left( f(a) + f(b) \right) \\ I_{n+1} &= \frac{I_n}{2} + h_{n+1} \sum_{i=1}^{2^{n-1}} f \left( a + (2i - 1)h_{n+1} \right) \\ R_{i,1} &= I_i \\ R_{i,j} &= R_{i,j-1} + \frac{R_{i,j-1} - R_{i-1,j-1}}{4^{j-1} - 1} \end{align*}\]

\(R_{n,n}\) is the answer!

Practice script

romb

## function (fx, a, b, N = 4) 
## {
##     R = matrix(nrow = N, ncol = N)
##     h = b - a
##     R[1, 1] = h/2 * (fx(a) + fx(b))
##     np = 1
##     for (i in 2:N) {
##         h = h/2
##         np = 2 * np
##         R[i, 1] = 1/2 * R[i - 1, 1] + h * sum(fx(a + h * seq(1, 
##             np - 1, 2)))
##         for (j in 2:i) {
##             R[i, j] = R[i, j - 1] + (R[i, j - 1] - R[i - 1, j - 
##                 1])/(4^(j - 1) - 1)
##         }
##     }
##     return(R[N, N])
## }
## <bytecode: 0x000001e2a3f4fd98>
## <environment: namespace:math>

fx = function(x) exp(-x/100)
format(romb(fx, 0, 24), digits=22)

## [1] "21.33721389334470330823"

fx2 = function(x) 3 * x * sin(x) - log(x)
format(romb(fx2, 0.8, 2.6), digits=22)

## [1] "6.887425952851619292971"

format(romb(fx2, 0.8, 2.6, N=8), digits=22)

## [1] "6.887419623354108288993"